移球游戏 (NOIP 2020)
Statement
You are playing a game which is about moving balls on poles.
There are $n + 1$ $(2 \leq n \leq 50)$ poles which are numbered from $1$ to $n + 1$. Initially, poles $1$ to $n$ each have $m$ $(2 \leq m \leq 400)$ balls on them. These $n \times m$ balls are colored in $n$ different colors, with $m$ balls of each color.
Initially, these balls are arbitrarily distributed. Your goal is to move all the balls of the same color onto a single pole. It does not matter which color ends up on which pole.
An operation allows you to move a ball from pole $x$ to pole $y$. You can perform an operation when the following conditions are satisfied:
- There is at least $1$ ball on pole $x$
- There is at most $m - 1$ balls on pole $y$
- You are moving the topmost ball from pole $x$ to the top of pole $y$
Accomplish your goal in at most $820000$ operations, and construct a valid sequence of operations.
| Subtask | Test Case | $n \leq$ | $m \leq$ |
|---|---|---|---|
| $1$ | $1 - 2$ | $2$ | $20$ |
| $2$ | $3 - 5$ | $10$ | $20$ |
| $3$ | $6 - 8$ | $50$ | $85$ |
| $4$ | $9 - 14$ | $50$ | $300$ |
| $5$ | $15 - 20$ | $50$ | $400$ |
Solution
There does not seem to be any immediately obvious way of solving the problem, so we start with subtask 1.
Subtask 1
In this subtask, $n = 2$. We aim to solve this subtask in $\mathcal{O}(m)$ operations.
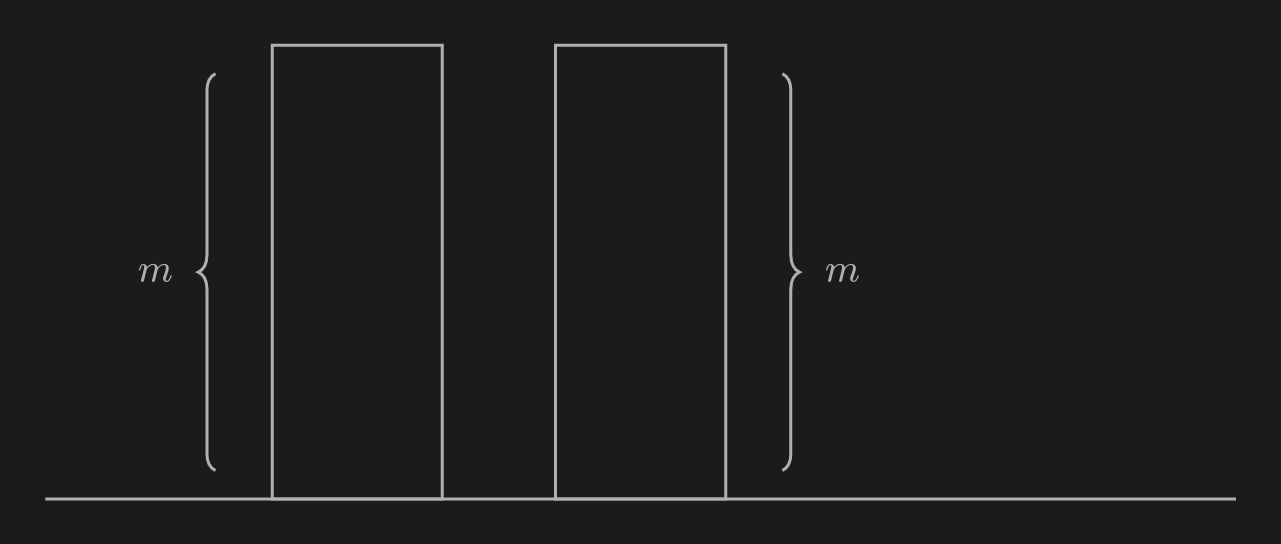
We will let the two colors be red and blue. After playing around with a couple examples, we come up with the following strategy:
Let $c$ denote the number of red balls on pole $1$.
Move the top $c$ balls from pole $2$ to pole $3$.
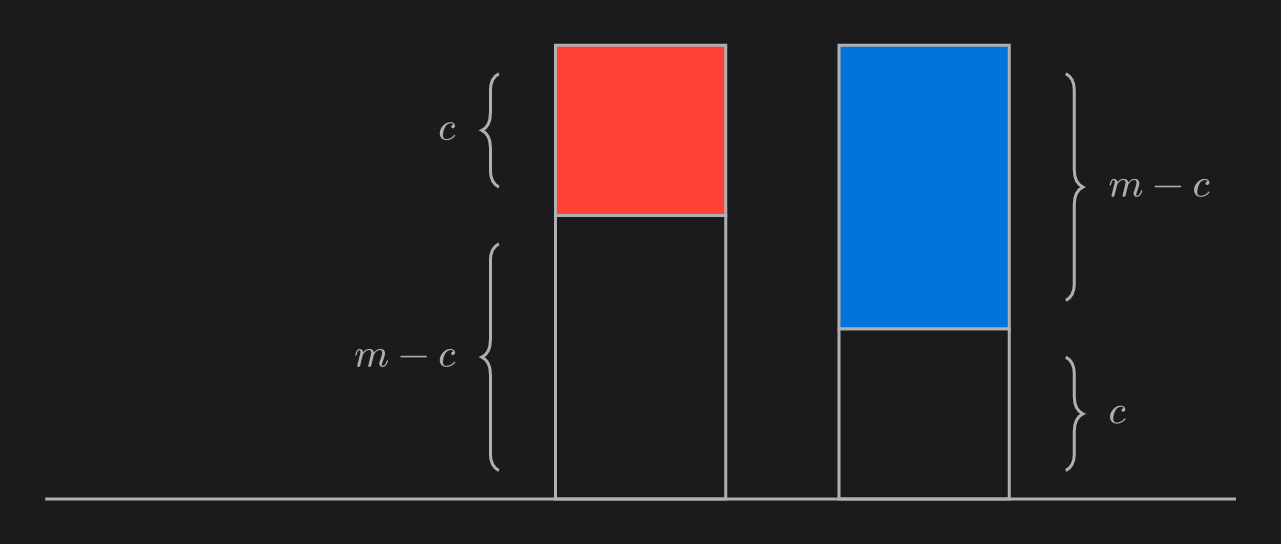
For each ball on pole $1$, move it to pole $2$ if it is red or pole $3$ if it is blue.
Move the $c$ red balls on pole $2$ back, then move the $m - c$ blue balls on pole $3$ back.
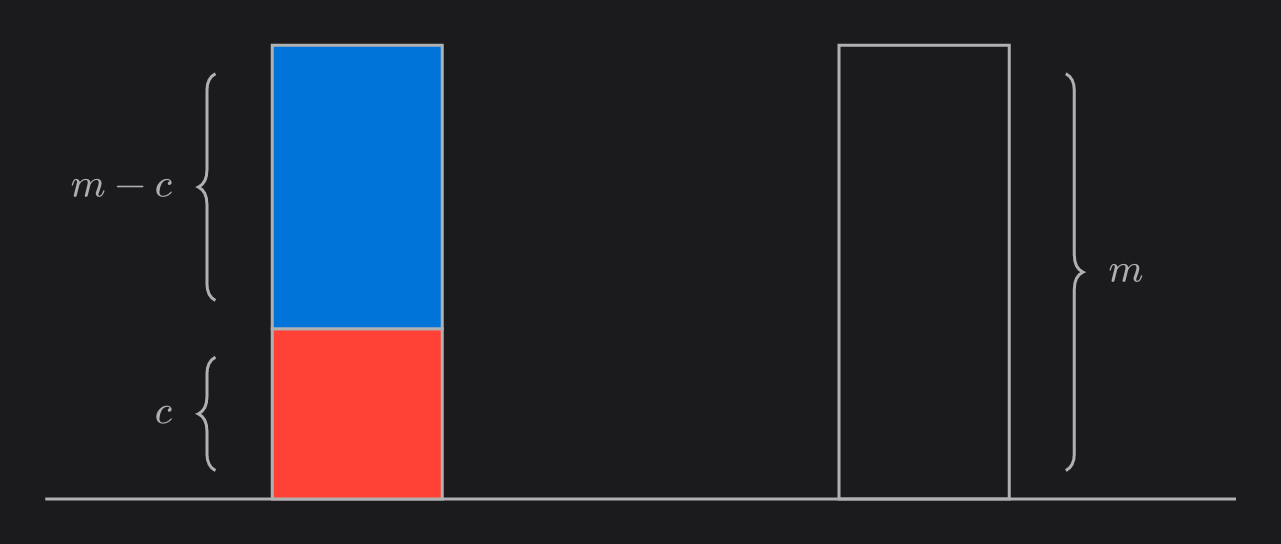
Move the remaining $m - c$ balls on pole $2$ to pole $3$.
Move the $m - c$ blue balls from pole $1$ to pole $2$.
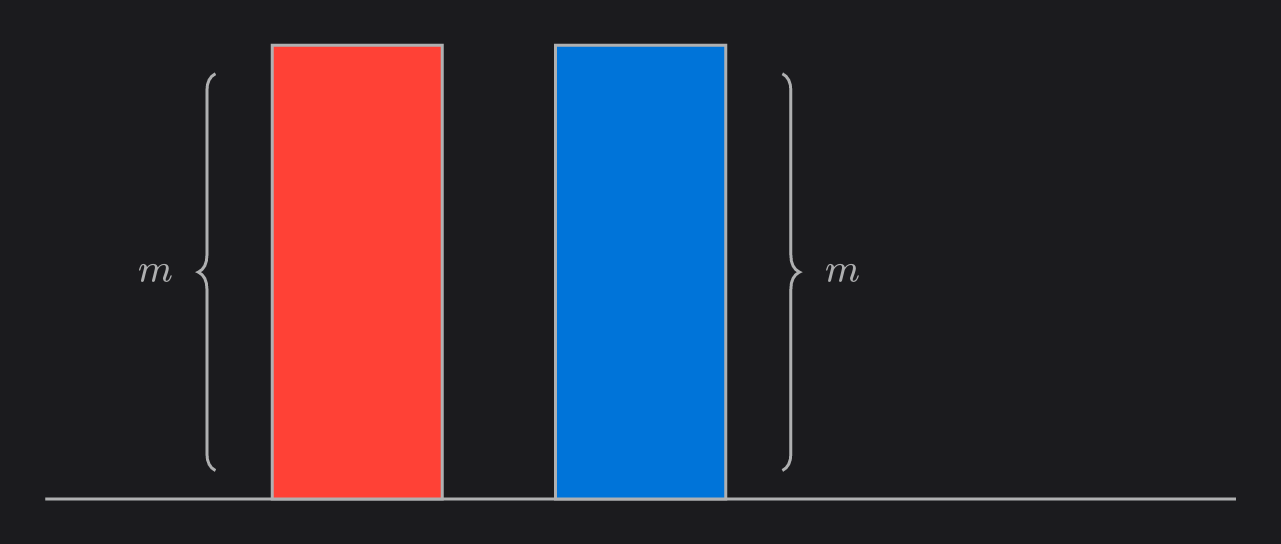
For each ball on pole $3$, move it to pole $1$ if it is red or pole $2$ if it is blue.
The number of operations in our construction is
\[c + m + c + (m - c) + (m - c) + (m - c) + m \leq 5m\]Note that the red balls always end up on pole $1$, and the blue balls on pole $2$. Additionally, even if the number of red balls and blue balls are different, at least one of the poles will be filled with same color balls if we move extra balls to the other pole in step 4.
Full Solution
Since it is hard to work with many colors at the same time, we try to use our solution for subtask 1.
Since we can solve the problem for 2 colors, we try divide and conquer, splitting our current colors into 2 groups each time. If we are solving the problem for the range of colors $[l, r)$, let $m = \lfloor \frac{l + r}{2} \rfloor$. For some color $c$, we assign it to be red if $c \lt m$, otherwise we assign it blue.
To partition some range $[i, j)$, we can start by applying the solution for $n = 2$ for poles $i$ and $j - 1$, and move inwards since at least one of the poles must be completed.
Once we complete our partition, we can recursively partition the ranges $[l, m)$ and $[m, r)$. Note that in our construction, $i = l$ and $j = r$ always hold, so implementing is simple.
Our construction passes comfortably as
\[T(n) = 2T(\frac{n}{2}) + 5mn\] \[T(n) = 5mn \log_{2} n \approx 600000\]Implementation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <algorithm>
#include <array>
#include <cstdint>
#include <ios>
#include <iostream>
#include <utility>
#include <vector>
template <typename F>
class y_combinator {
private:
F f;
public:
explicit y_combinator(F&& f) : f(f) {}
template <typename... Args>
decltype(auto) operator()(Args&&... args) const {
return f(*this, std::forward<Args>(args)...);
}
};
template <typename F>
y_combinator(F) -> y_combinator<F>;
void solve() {
using op_t = std::array<std::int32_t, 2>;
std::int32_t m;
std::int32_t n;
std::cin >> n >> m;
std::vector<std::vector<std::int32_t>> stks(n + 1);
for (std::int32_t i = 0; i < n; ++i) {
stks[i].resize(m);
for (auto& x : stks[i]) {
std::cin >> x;
--x;
}
}
std::vector<op_t> ops;
y_combinator(
[&](auto self, std::int32_t lo, std::int32_t hi) -> void {
const std::int32_t mi = (lo + hi) / 2;
const auto op = [&](std::int32_t x, std::int32_t y, std::int32_t tms) -> void {
for (std::int32_t i = 0; i < tms; ++i) {
stks[y].push_back(stks[x].back());
stks[x].pop_back();
ops.push_back(op_t({x, y}));
}
};
std::int32_t ptr_l = lo;
std::int32_t ptr_r = hi - 1;
while (ptr_l < ptr_r) {
std::int32_t cnt = 0;
for (auto x : stks[ptr_l]) {
cnt += x < mi;
}
op(ptr_r, n, cnt);
for (std::int32_t i = 0; i < m; ++i) {
op(ptr_l, stks[ptr_l].back() < mi ? ptr_r : n, 1);
}
op(ptr_r, ptr_l, cnt);
op(n, ptr_l, m - cnt);
op(ptr_r, n, m - cnt);
op(ptr_l, ptr_r, m - cnt);
for (std::int32_t i = 0; i < m; ++i) {
if (stks[n].back() < mi) {
op(n, std::int32_t(std::size(stks[ptr_l])) < m ? ptr_l : ptr_r, 1);
} else {
op(n, std::int32_t(std::size(stks[ptr_r])) < m ? ptr_r : ptr_l, 1);
}
}
ptr_l += *std::max_element(std::begin(stks[ptr_l]), std::end(stks[ptr_l])) < mi;
ptr_r -= *std::min_element(std::begin(stks[ptr_r]), std::end(stks[ptr_r])) >= mi;
}
if (mi - lo > 1) {
self(lo, mi);
}
if (hi - mi > 1) {
self(mi, hi);
}
}
)(0, n);
std::cout << std::size(ops) << '\n';
for (const auto& [x, y] : ops) {
std::cout << x + 1 << ' ' << y + 1 << '\n';
}
}
int main() {
std::cin.tie(nullptr);
std::ios_base::sync_with_stdio(false);
solve();
return 0;
}